Како промијенити време и опсег тела
Како промијенити време и опсег тела
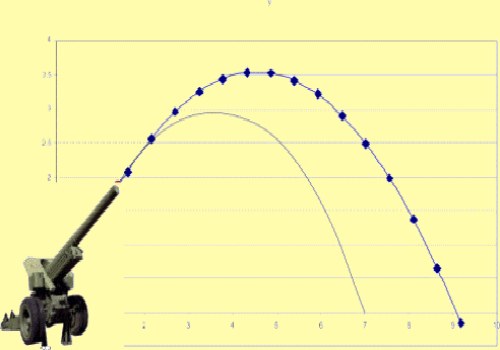
Покрет тела, бачена под углом према хоризонту, описана је у две координате. Једна карактеризира растојање Лет, а друга - висина. Време лета зависи од максималне висине коју тело достиже.

Инструкције
1
2
Угао α, под којим се тело баци, није наведенслучајно. Кроз то можете написати почетну брзину у координатним осама. Дакле, в0 (к) = в0 · цос (α), в0 (и) = в0 · син (α). Сада можемо добити функцију координатних компоненти брзине: в (к) = цонст = в0 (к) = в0 · цос (α), в (и) = в0 (и) -г · т = в0 · син (α) -г · т.
3
Координате тела к и и зависе од времена т. Тако можемо формирати две једначине зависности: к = к0 + в0 (к) · т + а (к) · т² / 2, и = и0 + в0 (и) · т + а (и) · т² / 2. Пошто к0 = 0 и а (к) = 0 хипотезом, имамо к = в0 (к) · т = в0 · цос (α) · т. Такође је познато да је и0 = 0, а (и) = - г (знак минуса се појављује зато што је правац гравитационог убрзања г и позитивног правца Ои оси супротан). Дакле, и = в0 · син (α) · т-г · т² / 2.
4
Време лета може се изразити из брзине,знајући да се у максималној тачки тело зауставља тренутачно (в = 0), а "пораст" и "спуст" времена су једнаки. Дакле, ако заменимо в (и) = 0 у једначину в (и) = в0 · син (α) -г · т, добијамо 0 = в0 · син (α) -г · т (п), где је т (п) - максимално време, "т вертек". Отуда т (п) = в0 · син (α) / г. Укупно време лета се тада изражава као т = 2 · в0 · син (α) / г.
5
Иста формула се може добити на други начин,математички, из једначине за координату и = в0 · син (α) · т-г · т² / 2. Ова једначина може бити преписана у незнатно модификованом облику: и = -г / 2 · т² + в0 · син (α) · т. Видјено је да је ово квадратна зависност, где је и функција, т је аргумент. Врха параболе која описује путању је тачка т (п) = [- в0 · син (α)] / [- 2г / 2]. Минусе и деуцес су скраћени, тако да је т (п) = в0 · син (α) / г. Ако означимо максималну висину за Х и подсећамо да је врхна тачка вертикала параболе дуж кога се тело помера, онда је Х = и (т (п)) = в0²син² (α) / 2г. То јест, да бисте добили висину, неопходно је "т вертек" у једнацини за координатну и.
6
Дакле, време лета је написано каот = 2 · в0 · син (α) / г. Да бисте је променили, морате сходно томе променити почетну брзину и угао нагиба. Што је већа брзина - дуже тело лети. Угао је нешто компликованији, јер време не зависи од самог угла, већ од његовог синуса. Максимална могућа вредност сине - јединице - постиже се под углом од 90 °. То значи да тело путује најдуже време када се баци вертикално нагоре.
7
Распон лета је коначна координата к. Ако заменимо наћи већ налета једначине к = в0 · јер (ниво а) · т, лако је наћи тај Л = 2в0²син (α) цос (α) / г,. Могу се применити тригонометриц конфигурација доубле угла 2син (α) цос (α) = син (2а), тада Л = в0²син (2а) / г. Синус два алфа једнака када 2а = н / 2, а = н / 4. Тако, максимално растојање лета у случају ако се тело баци на 45 °.