Савет 1: Како израчунати модул броја
Савет 1: Како израчунати модул броја
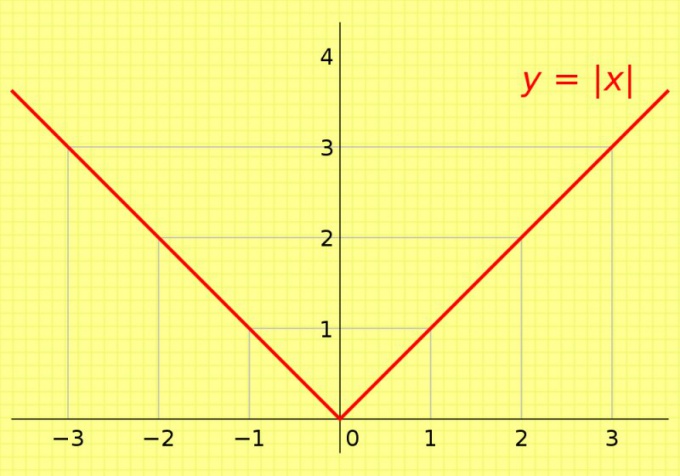
Модул број Апсолутна вредност, која се пише коришћењем вертикалних заграда: | к |. Може се визуализовати као интервал, постављен у било ком смеру од нуле.

Инструкције
1
Ако је модул приказан као непрекиданфункција, вриједност његовог аргумента може бити позитивна или негативна: | к | = к, к ≥ 0; | к | = - к, к <0. Због тога број који се налази у заградама узима сваки знак.
2
Модул нуле је нула, а модул било когпозитивни број за њега. Ако је аргумент негативан, након израза заграда, његов знак се мења из минуса на плус. На основу тога, следи да су модули супротних бројева једнаки | -к | = | к | = к.
3
Модул комплексног броја се може наћи по формули: | а | = √б ² + ц ², и | а + б | ≤ | а | + | б |. Ако аргумент садржи позитиван цијели број као множитељ, онда се може извадити знак знакова, на пример: | 4 * б | = 4 * | б |.
4
Модул не може бити негативан, тако да се сваки негативни број претвори у позитиван: | -к | = к, | -2 | = 2, | -1/7 | = 1/7, | -2,5 | = 2.5.
5
Ако је аргумент представљен као комплексан број,онда је због погодности калкулације дозвољено да промени редослијед израза затворених у правоугаоне заграде: | 2-3 | = | 3-2 | = 3-2 = 1, будући да је (2-3) мања од нуле.
6
Повишени аргумент је истовремено под коријенским знаком истог редоследа - решен је уз помоћ модула: √а² = | а | = ± а.
7
Ако имате задатак који не укључујеуслов за проширење заграда модула, не морате да их се решите - то ће бити крајњи резултат. И ако желите да их откријете, потребно је да наведете знак ±. На пример, морате пронаћи вриједност израза √ (2 * (4-б)) ². Његово решење изгледа овако: √ (2 * (4-б)) ² = | 2 * (4-б) | = 2 * | 4-б |. Пошто је знак израза 4-б непознат, он мора остати у заградама. Ако додамо додатни услов, на пример, | 4-б | > 0, а на крају добијамо 2 * | 4-б | = 2 * (4 - б). Као непознати елемент може се одредити и одређени број, који треба узети у обзир, пошто то ће утицати на знак израза.
Савет 2: Како пронаћи модул броја
Модул број н је број сегментних јединица од порекла до тачке н. И није битно у ком правцу ће се то одстојање мјерити - десно или лијево од нуле.

Инструкције
1
Модул број такође се зове апсолутна вредност овог број. Означава се кратким вертикалним линијама повученим лево и десно од број. На пример, модул број 15 се пише на следећи начин: | 15 |.
2
Запамтите да модул може бити само позитиван број или нула. Модул позитивно број је једнак самом броју. Модул нула је једнака нули. То је, за било које број н, која је већа или једнака нули, следи формула: | н | = н. На пример, | 15 | = 15, то јест модул број 15 је једнако 15.
3
Негативан број бити исти број, али са супротним знаком. То је, за било које број н, што је мање од нуле, формула | н | = -н. На примјер, | -28 | = 28. Модул број -28 је једнако 28..
4
Модуле можете пронаћи не само за интегерс, већ и за делимичне бројеве. Иста правила важе за делимичне бројеве. На пример, | 0,25 | = 25, то јест, модул број 0,25 ће бити једнако 0,25. А | -2 | = ¾, то јест, модул број -¾ бити једнако ¾.
5
Када радите са модулима, корисно је знати да су модули супротних бројева увек једнаки једни другима, то јест, | н | = | -н |. Ово је главно својство модула. На пример, | 10 | = | -10 |. Модул број 10 је 10, баш као и модул број -10. Осим тога, | а - б | = | б - а |, пошто су растојање од тачке а до тачке б и растојања од б до а једнаке једна другој. На пример, | 25 - 5 | = | 5 - 25 |, то јест, | 20 | = | - 20 |.
Савет 3: Како израчунати сложене бројеве
Комплексни бројеви - даље ширење концептабројеве у односу на стварне бројеве. Увод у математику сложених бројева омогућио је да дају готову форму многим законима и формулама, а такође су открили дубоке везе између различитих области математичке науке.

Инструкције
1
Као што је познато, ниједан стварни број нијеможе бити квадратни корен негативног броја, то јест, ако је б <0, онда је немогуће наћи а такав да је а ^ 2 = б. У вези с тим, одлучено је увести нову јединицу помоћу које би могли изразити такав. Зове се имагинарна јединица и ознака и. Замишљена јединица је једнака квадратном корену од -1.
2
Пошто и ^ 2 = -1, онда је √ (-б ^ 2) = √ ((- 1) * б ^ 2) = √ (-1) * √ (б ^ 2) = иб. Тако је уведен концепт имагинарног броја. Сваки имагинарни број се може изразити као иб, где је б стваран број.
3
Прави бројеви могу бити представљени у обликунумеричка осовина од минус бесконачности до плус бесконачности. Било је погодно да се представи имагинарни бројеви у облику аналогном оси која је правоугаона према оси реалних бројева. Заједно, они чине координате нумеричке равни.У овом случају, за сваку тачку нумеричке равни са координатама (а, б) одговара један и само један комплексни број облика а + иб, где су аи б стварни бројеви. Први израз ове суме назива се прави део комплексног броја, други израз назива имагинарни део.
4
Ако је а = 0, онда је комплексни број назван чисти имагинарни. Ако је б = 0, онда се број зове реалан.
5
Знак додавања између стварног и имагинарногделови комплексног броја не означавају њихову аритметичку сума. Уместо тога, комплексни број може бити представљен као вектор чије порекло се поклапа са пореклом, а крај је у (а, б). Као иу сваком вектору, комплексни број има апсолутну вриједност или модул. Ако је з = к + ии, онда | з | = √ (к2 + и ^ 2).
6
Два сложена броја се сматрају једнака само уако стварно део једнак реалног дела и један имагинарни део друга је имагинарни део оног другог, то је: З1 = З2, ако је к1 = к2 и и1 = и2.Однако за комплексним бројевима немају смисла за неједнакости знакова, који не значи да z1 <З2 и z1> з 2. Упоредите на овај начин могу само модули комплексних бројева.
7
Ако су з1 = к1 + ии1 и з2 = к2 + ии2 комплекснебројеви, па: з1 + з2 = (к1 + к2) + и (и1 + и2), з1 - з2 = (к1 - к2) + и (и1 - и2); лако увидети да додавање и одузимање комплексних бројева следи исти пресуди да сабирање и одузимање вектора.
8
Производ два комплексних бројева једнак: з1 * з2 = (к1 + ии1) * (к2 + ии2) = к1 * к2 + и * и1 * к2 + и * к1 * и2 + (и ^ 2) * и1 * и и2.Посколку ^ 2 = -1, онда је крајњи резултат је: (к1 * к2 - и1 * и2) + и (к1 * и2 + к2 * и1).
9
Операције експозиционирања и екстракција кореназа сложене бројеве се дефинишу на исти начин као и за стварне бројеве. Међутим, у комплексном домену за било који број постоје тачно н бројеви б такви да је б ^ н = а, то јест, н корени н-ове моћи. То посебно значи да свака алгебарска једначина н-та с једне варијабле има тачно н комплексни корени, од којих неки могу бити валидни.
Савет 4: Како додати број корену
Корен је икона која означаваматематичка операција проналажења таквог броја, чија је ерекција у степену који је назначен прије знакова корена, треба да дају број наведен под овим знаком. Често, да би решили проблеме у којима постоје коријени, није довољно само израчунати вриједност. Морамо извршити додатне операције, од којих је једна додавање броја, варијабле или израза у роот знак.

Инструкције
1
Одредите експонента корена. Индикатор звао цео број који указује на степен у којем је неопходно да се подигне резултат обрачуна корена, да добије радицанд (број из којег се уклања корен). Експонент корена је написан као експонирање икону корена. Ако индекс није одређен, то значи кореновање, чији обим је једнака два. На пример, индекс корен √3 је два, три дисплаи ³√3 једнаки, индекс корена је четири ⁴√3 етц.
2
Подигните број који желите подићикорен знак, до једнаке експоненту овог корена, као што сте одредили у претходном кораку. На пример, ако желите да унесете број 5 испод главног знака ⁴√3, онда је експонент роот-а 4 и морате израчунати резултат подизања 5 на четврту снагу 5-4 = 625. Можете то учинити на било који начин - на уму, помоћу калкулатора или релевантних онлине услуга, постављених на Интернет.
3
Унесите вредност добијена у претходном коракупод коријенским знаком као мултипликатор радиканд експресије. За пример који се користи у претходном кораку, уз додавање броја 5 (5 * ⁴√3) у корен ⁴3, ова акција се може писати као: 5 * ⁴√3 = ⁴ (625 * 3).
4
Поједностављену изведену радиканцу, акоово је могуће. За пример из претходних корака то значи да морате само множити бројеве испод роот знакова: 5 * ⁴√3 = ⁴√ (625 * 3) = ⁴√1875. Ово довршава операцију уноса броја под корен.
5
Ако у проблему постоје непознати подациваријабле, горњи кораци могу обавити у општој форми. На пример, ако желите да направите четврту корен непознате променљиве к, радикални израз једнак 5 / Кс³, цела секвенца акција може написати као: к * ⁴√ (5 / Кс³) = ⁴√ (к⁴ * 5 / Кс³) = ⁴√ (к * 5).
Савет 5: Како пронаћи модул комплексног броја
Реални бројеви нису довољнирешити било коју квадратну једначину. Најједноставније од квадратних једначина које немају корене међу стварним бројевима је к ^ 2 + 1 = 0. Када се то реши, испада да је к = ± скрт (-1), ау складу са законима елементарне алгебре, екстракт корена парног степена од негативног број то је немогуће.

Требаће вам
- - папир;
- - дршка.
Инструкције
1
У овом случају постоје два начина: прво је пратити утврђене забране и претпоставити да ова једначина нема корене; Друга је да се систем реалних бројева проширује до те мере да ће једначина имати корен. Тако се појавио појам сложених бројева обрасца з = а + иб, у којем је (и ^ 2) = - 1, гдје је и имагинарна јединица. Бројеви а и б се зову, респективно, стварни и имагинарни делови број з Рез и Имз. Важна улога у акцијама са сложеним бројиграју број комплексни коњугат. Коњугат комплексног броја з = а + иб се зс = а-иб, тј. Број који има супротан знак испред имагинарне јединице. Дакле, ако је з = 3 + 2и, онда зс = 3-2и. Сваки стварни број је посебан случај комплекса број, имагинарни део је нула. 0 + и0 је комплексни број једнак нули.
2
Свеобухватно број може се додати и помножити на исти начин као и ововезе са алгебарских израза. У том случају, уобичајени закони сабирања и множења остају на снази. Нека З1 = А1 + ИБ 1, З2 = а 2 + иб2.1. Аддитион анд вицхитание.з1 + з2 = (а1 + а2) + и (б1 + б2), з1-з2 = (а1-а2) + и (б1-б2). 2. Умнозхение.з1 * з2 = (а1 + иб1) (а2 + ИБ2) = А1А2 + иа1б2 + иа2б1 + (и ^ 2) б1б2 = (А1А2-б1б2) + и (А1Б2 + а2б1) .Ако умножен једноставно отворене брацкетс анд применити дефиницију и ^ 2 = -1. Производ Коњугат комплексни број је реалан број: з * ЗС = (а + иб) (а-иб) == а ^ 2- (и ^ 2) (б ^ 2) = а ^ 2 + б ^ 2.
3
3. Дивизија.Довести приватну З1 / З2 = (А1 + иб1) / (А2 + ИБ2) у стандардној форми да се ослободи од замишљеног јединице у именилац. За ово најлакше умножи бројник и именилац од коњугата именилац: ((а1 + иб1) (а2-ИБ2)) / ((а2 + ИБ2) (а2-ИБ2)) = ((А1А2 + б1б2) + И (а2б1 -а1б2)) / (а ^ 2 + б ^ 2) = = (А1А2 + б1б2) / (а ^ 2 + б ^ 2) + и (а2б1-А1Б2) / (а ^ 2 + б ^ 2) .Оператсии сабирање и одузимање, као множење и дељење су међусобно инверзна.
4
5
Са сваком тачком з комплексне равни, радијус вектор ове тачке је повезан. Дужина радијус вектора који представља комплексни број з назива се модул р = | з | интегрирано број; и угао између позитивног правца реалне осе и правца вектора 0З се назива аргумент аргз овог комплекса број.
6
Аргумент комплекса број сматра се позитивним ако се рачунапозитиван правац оси 0к у супротном смеру казаљке на сату, а негативан у супротном правцу. Један комплексни број одговара скупу вриједности аргумента аргз + 2нк. Из ових вриједности сматра се да су вриједности аргз-а, у распону од -н до н, главне. Коњугатски комплекс број З и зс имају једнаке модуле, а њихови аргументи су једнаки у апсолутној вредности, али се разликују у знаку.
7
Дакле, | з | ^ 2 = а ^ 2 + б ^ 2, | з | = скрт (а ^ 2 + б ^ 2). Дакле, ако је з = 3-5и, онда | з | = скрт (9 + 25) = 6. Поред тога, пошто з * зс = | з | ^ 2 = а ^ 2 + б ^ 2, постаје могуће израчунати модули читавих комплексних израза у којима се имагинарна јединица може појавити више пута. Пошто је з = (1-3и) ( 4 + и) / (2-2и) = 9/2-и, директни прорачун модула з даје | з | ^ 2 = 81/4 + 1 = 85/4 и | з | = скрт (85) / 2. Пролазимо кроз фазу израчунавања, узимајући у обзир да зс = (1 + 3и) (4-и) / (2 + 2и) можемо написати: | з | ^ 2 = з * зс == (1-3и) (1 + 3и (4 + и) (4-и) / ((2-2и) (2 + 2и)) = (1 + 9) (16 + 1) / (4 + 4) = 85/4 и | з | = скрт (85) / 2.
Савет 6: Како додати модул
Модул - она је интегрални део укупне, нечије целине. Модул се може додати или уклонити без уништења главног језгра. Модул може бити програм, део уређаја. Сличан дизајн се користи, на пример, у оперативном систему Линук. Модуларна архитектура има Линук кернел.

Требаће вам
- - ПЦ;
- - Линук оперативни систем.
Инструкције
1
Да бисте додали или уклонили модуле у Линук оперативном систему, постоје посебне команде и модпробе програм. Сама Линук кернела садржи многе кодове који подржавају једну или другу вриједност.
2
Сви модули се налазе у посебном директоријуму/ либ / модулес / $ (унаме -р). Додајте или уклоните модул из Линук кернела модпробе командом. Прво унесите корисничку лозинку и пријавите се као администратор.
3
Стандардна командна линијакод изгледа отприлике овако: [лех @ лоцалхост лех] #. Команда за додавање модула мора се унети овако: судо модпробе вбокдрв. Затим пронађите потребан модул на вашем Линук систему.
4
Сви главни модули морају бити учитаниаутоматски. Ако, након инсталирања неког хардвера, и даље морате додати модул кернела, програм Кудзу би требао започети. Он ће утврдити да ли ова опрема подржава систем и конфигурише свој модул. Да бисте сазнали да ли је модул успешно додан, користите наредбу / сбин / лсмод.