Савет 1: Како пронаћи градијент функције
Савет 1: Како пронаћи градијент функције
Градијент функција Је векторска количина, чија је одређеност повезана са одређивањем парцијалних деривата функције. Правац градијента указује на пут најбрже расту функције из једне тачке скаларног поља на други.

Инструкције
1
Да решите проблем на градијенту функцијеКористе се методе диференцијалног рачунања, односно одређивање парцијалних деривата првог реда у три варијабле. Овде се претпоставља да функција и сви његови парцијални деривати имају својство континуитета у домену дефиниције функције.
2
Градијент је вектор чији правацуказује на правац максимално брзог пораста функције Ф. За ово, на графу су изабране две тачке М0 и М1, које су крајеви вектора. Величност градијента је једнака брзини повећања функције од тачке М0 до тачке М1.
3
Функција је диференцибилна на свим тачкама овогавектор, дакле, сви његови парцијални деривати су пројекције вектора на координатним осама. Тада градијентна формула изгледа овако: град = (∂Ф / ∂к) • и + (∂Ф / ∂и) • ј + (∂Ф / ∂з) • к, где су и, ј, к координате јединичног вектора. Другим речима, градијент функције је вектор чије су координате његове парцијалне деривате град Ф = (∂Ф / ∂к, ∂Ф / ∂и, ∂Ф / ∂з).
4
Пример 1. Нека се дода функција Ф = син (к • з²) / и. Потребно је пронаћи свој градијент у тачки (π / 6, 1/4, 1).
5
Решење: Дефинишите парцијалне деривате у односу на сваку варијаблу: Ф'_к = 1 / и • цос (к • з²) • з²; Ф'_и = син (к • з²) • (-1) • 1 / (и²) _з = 1 / и • цос (к • з²) • 2 • к • з.
6
Замените познате вредности координата тачке: Ф'_к = 4 • цос (π / 6) = 2 • √3; Ф'_и = син (π / 6) • (-1) • 16 = -8; Ф'_з = 4 • цос (π / 6) • 2 • π / 6 = 2 • π / √3.
7
Примијенити формулу градијента функције: град Ф = 2 • √3 • и - 8 • ј + 2 • π / √3 • к.
8
Пример 2. Пронађите координате градијента функције Ф = и • арстг (з / к) у тачки (1, 2, 1).
9
Решење.(З / к) + и • (арцтг (з / к)) 'к = и • 1 / (1 + (з / к) 2) • (-з / к²) = -и • з / (к2 • (1 + (з / к) ²)) = -1; Ф'_и = 1 • арцтг (з / к) = арцтг 1 = π / 4; Ф'_з = 0 • арцсг (з (1 / к) + и • (арцтг (з / к)) 'з = и • 1 / (1 + (з / к) 2) • 1 / к = и / (к • (1 + (з / к) 2 )) = 1.град = (-1, π / 4, 1).
Савет 2: Како пронаћи градијент скаларног поља
Градијент скаларног поља је векторска количина. Дакле, да би је пронашли, потребно је одредити све компоненте одговарајућег вектора, почевши од знања о расподели скаларног поља.

Инструкције
1
Прочитајте у уџбенику о вишој математиције градијент скаларног поља. Као што је познато, ова векторска количина има правац карактерисан максималном стопом пада скаларне функције. Овај осећај датог вектора је оправдан изразом за одређивање његових компоненти.
2
Запамтите да је било који вектор одређен количиномњегова компонента. Компоненте вектора су заправо пројекције овог вектора на једну или другу координатну осу. Дакле, ако се разматра тродимензионални простор, вектор мора имати три компоненте.
3
Запишите како се одређују компоненте вектора,што је градиент неког поља. Свака од координата таквог вектора једнака је деривату скаларног потенцијала у односу на варијаблу, која је израчуната координата. То јест, ако је потребно израчунати компоненту "Ик" векторског градијента вектора, онда је неопходно разликовати скаларну функцију у варијабли "к". Имајте на уму да дериват мора бити приватан. То значи да, када се разликују, преостале варијабле које не учествују у њему морају се сматрати константама.
4
Напишите израз за скаларно поље. Као што знате, овај термин имплицира само скаларну функцију од неколико варијабли, која су такође и скаларне величине. Број варијабли скаларне функције ограничен је димензијом простора.
5
Диференцијација одвојене скаларне функције од странесвака варијабла. Као резултат, добићете три нове функције. Напишите сваку функцију у изразу за вектор градијента скаларног поља. Свака од добијених функција је заправо коефицијент за јединични вектор дате координате. Стога, коначни градијентни вектор би требао изгледати као полином са коефицијентима у облику деривативних функција.
Савет 3: Како пронаћи градијент
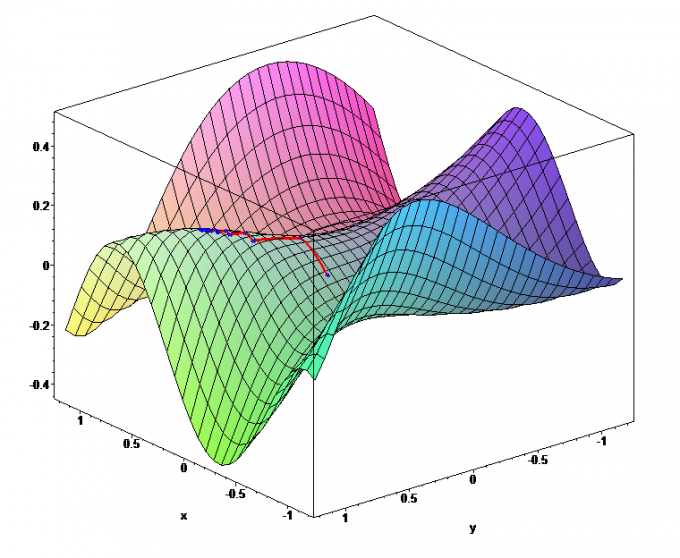
Када се разматрају питања која укључују концепт градијента, функције се обично перципирају као скаларна поља. Стога је неопходно увести одговарајућу нотацију.
Требаће вам
- - Боом;
- - дршка.
Инструкције
1
Нека је функција дати са три аргумента у = ф (к,и, з). Парциални дериват функције, на пример у односу на к, дефинисан је као дериват који се односи на овај аргумент, добијен са преосталим аргументима. За остале аргументе је слично. Нотација парцијалног деривата пише у облику: дф / дк = у'к ...
2
Укупни диференцијал ће бити једнак са ду = (дф / дк) дк +(дф / ди) ди + (дф / дз) дз. Парцијални деривати могу се схватити као деривати у правцима координатних осе. Стога поставља се питање проналаска деривата у односу на смер датог вектора с у тачки М (к, и, з) (не заборавите да правац с специфицира вектор јединичне векторске јединице с ^ о). У овом случају, вектор-диференцијација аргумената {дк, ди, дз} = {дсцос (алпха), дсос (бета), дсос (гамма)}.
3
Узимајући у обзир облик укупног диференцијалног ду,закључити да је дериват правац-нију с у тачки М је једнак: (ду / ДС) | М = ((ДФ / дк) | М) цос (алфа) + ((дф / ди) | М) цос (бета) + ((дф / дз) | М) цос (гамма). Ако је с = с (ск, си, сз), онда су израчунати цосинес {цос (алпха), цос (бета), цос (гамма)} (видети Сл. 1а).

4
Дефиниција деривата у односу на правац, претпоставља сетачка М варијабле можемо записати као скаларни производ: (ду / ДС) = ({дФ / дк, дф / ди, дф / ЗВ}, {цос (алпха), цос (бета) цос (гама)}) = (град у, с ^ о). Овај израз ће бити валидан за скаларно поље. Ако узмемо у обзир функцију-тион, градф - вектор који координате поклапају делимични ф (к, и, з) .градф (к, и, з) = {{дф / дк, дф / Ди, дф / = дз}) = (дф / дк) и + (дф / ди) ј + (дф / дз) к. Овде, (и, ј, к) - вектори правоугли координатни оса у правоуглом координатном систему.
5
Ако користите диференцијалвектор Хамилтоновог оператора, онда градф може се написати као умножавање овог вектора оператора скаларним ф (види Слику 1б). Са становишта везе градф ц у односу на правац, једнакост (градф, с ^ о) = 0 је могућа ако су ови вектори ортогонални. Стога градф се често дефинише као правац најбрже промене у скаларном пољу. И са становишта диференцијалних операција (градф је један од њих), својства градфа тачно понављају својства диференцирања функција. Посебно, ако је ф = ув, онда градф = (вград + у град).
Савет 4: Како нацртати градијент
Градијент То је алат у графичким уредницима који врши попуњавање контуре глатком преласком једне боје у другу. Градијент може дати контуру ефекат запремине, симулиратиосветљење, одсјај светлости на површини објекта или ефекат заласка сунца у позадини фотографије. Овај алат се широко користи, тако да је веома важно научити како га користити за обраду фотографија или креирање илустрација.
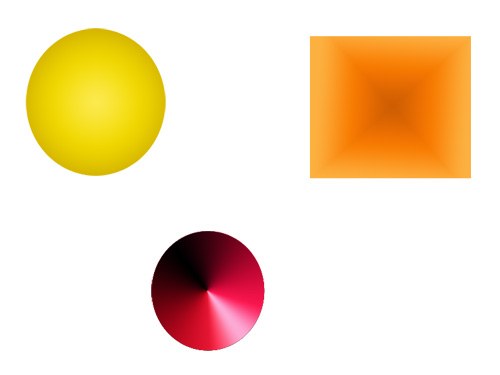
Требаће вам
- Рачунар, графички едитор Адобе Пхотосхоп, Цорел Драв, Паинт.Нет или други.
Инструкције
1
Отворите слику у програму или креирајте нову. Креирајте путању или изаберите жељену област на слици.
2
Укључите алат за градијент на траци са алаткамаалати графичког уређивача. Поставите показивач миша на тачку унутар изабраног подручја или контуре, у којем ће почети прва боја градијента. Притисните и држите леви тастер миша. Померите курсор до тачке где би градијент требало да иде до последње боје. Откажите леви тастер миша. Изабрана стаза ће попунити градијент.
3
ГрадијентМожете одредити транспарентност, боје и њиховеоднос на одређеном месту преливања. Да бисте то урадили, отворите прозор за уређивање градијента. Да бисте отворили прозор за уређивање у Пхотосхоп-у, кликните на узорак градијента на панелу "Опције".
4
У отвореном прозору, у виду примера, приказују се расположиве опције за попуњавање градијента. Да бисте уредили неку од опција, изаберите га кликом миша.
5
Узорак се приказује на дну прозораградијент у облику широке скале на којој се налазе клизачи. Клизачи указују на тачке у којима градијент треба да има наведене карактеристике, а у интервалу између клизача боја излази равномерно од друге тачке наведене у првој тачки.
6
Клизачи који се налазе на врхуСкале постављају транспарентност градијента. Да бисте променили транспарентност, кликните на жељени клизач. По скали се појављује поље у којем уносите жељени степен транспарентности у процентима.
7
Клизачи на дну скале означавају боје градијента. Кликом на једну од њих, можете одабрати жељену боју.
8
Градијент може имати неколико прелаза боја. Да бисте одредили другу боју - кликните на слободни простор на дну скале. На њему ће бити још један клизач. Наведите жељену боју за то. Скала ће приказати узорак градијента са још једним тачком. Клизаче можете премјестити држећи их лијевим тастером миша да бисте остварили жељену комбинацију.
9
ГрадијентПостоји неколико врста које могу датиоблик равних контура. На пример, да би се круг у облику кугле користио, користи се радијални градијент, а да се добије облик конуса, он је коничан. Да би се површини појавила илузија конвексности, можете користити градијент огледала, а градијент у облику дијаманта може се користити за стварање врхунаца.







